Triunghiuri de tensiuni, rezistențe și puteri
Oricine are o idee despre diagramele vectoriale va observa cu ușurință că un triunghi de tensiune în unghi drept poate fi distins foarte clar pe ele, fiecare parte a căruia reflectă: tensiunea totală a circuitului, tensiunea rezistenței active și tensiunea. asupra reactanței.
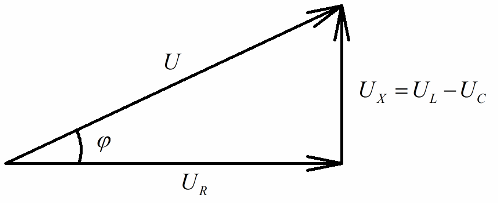
În conformitate cu teorema lui Pitagora, relația dintre aceste tensiuni (între tensiunea totală a circuitului și tensiunea secțiunilor sale) va arăta astfel:
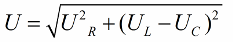
Dacă următorul pas este împărțirea valorilor acestor tensiuni la curent (curentul trece în mod egal prin toate secțiunile circuitului în serie), atunci prin Legea lui Ohm obținem valorile rezistenței, adică acum putem vorbi despre un triunghi dreptunghic de rezistențe:
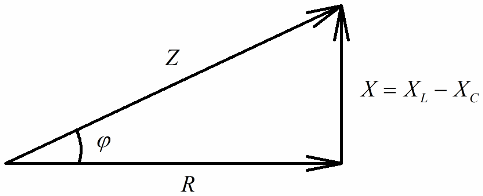
Într-un mod similar (ca și în cazul tensiunilor), folosind teorema lui Pitagora, se poate stabili o relație între impedanța circuitului și reactanțele. Relația va fi exprimată prin următoarea formulă:
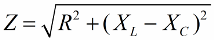
Apoi înmulțim valorile rezistenței cu curentul, de fapt vom crește fiecare latură a triunghiului dreptunghic de un anumit număr de ori. Ca rezultat, obținem un triunghi dreptunghic cu capacități:
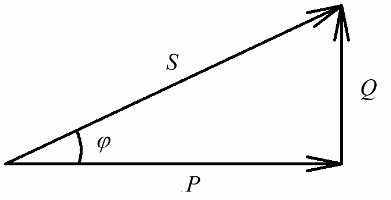
Puterea activă eliberată la rezistența activă a circuitului asociată cu conversia ireversibilă a energiei electrice (în căldură, în efectuarea lucrărilor în instalație) va fi în mod clar legată de puterea reactivă implicată în conversia reversibilă a energiei (crearea de câmpuri magnetice şi electrice în bobine şi condensatoare) şi cu putere maximă furnizată instalaţiei electrice.
Puterea activă se măsoară în wați (W), puterea reactivă — în varis (VAR — volt-amperi reactiv), totală — în VA (volt-amperi).
Conform teoremei lui Pitagora, avem dreptul de a scrie:
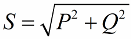
Să acordăm acum atenție faptului că în triunghiul puterii există un unghi phi, al cărui cosinus este ușor de determinat în primul rând prin puterea activă și puterea aparentă. Cosinusul acestui unghi (cos phi) numit factor de putere. Acesta arată cât de mult din puterea totală este contabilizată atunci când se efectuează lucrări utile într-o instalație electrică și nu este returnată la rețea.
Evident, un factor de putere mai mare (unul maxim) indică o eficiență de conversie mai mare a energiei livrate centralei pentru funcționare. Dacă factorul de putere este 1, atunci toată energia furnizată este folosită pentru a lucra.
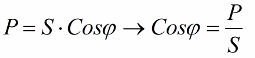
Rapoartele obținute permit exprimarea consumului de curent al instalației în termeni de factor de putere, putere activă și tensiune de rețea:
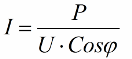
Deci, cu cât cosinusul phi este mai mic, cu atât este necesar mai mult curent de către rețea pentru a face o anumită lucrare. În practică, acest factor (curent maxim de rețea) limitează capacitatea de transmisie a liniei de transmisie și, prin urmare, cu cât este mai mic factorul de putere, cu atât este mai mare sarcina liniei și cu atât este mai mică lățimea de bandă utilă (cosinusul phi scăzut duce la restricție). Pierderile în joule în liniile electrice cu cosinus phi descrescătoare pot fi observate din următoarea formulă:
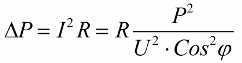
Pe rezistența activă R a liniei de transmisie, pierderile cresc cu cât curentul I este mai mare, deși este reactiv la sarcină. Prin urmare, putem spune că, cu un factor de putere scăzut, costul transportului de energie electrică pur și simplu crește. Aceasta înseamnă că creșterea cosinus phi este o sarcină economică națională importantă.
Este de dorit ca componenta reactivă a puterii totale să se apropie de zero.Pentru a face acest lucru, ar fi bine să folosiți întotdeauna motoare electrice și transformatoare la sarcină maximă și să le opriți la sfârșitul utilizării, astfel încât să nu funcționeze în gol. Fără sarcină, motoarele și transformatoarele au un factor de putere foarte scăzut. O modalitate de a crește cosinusul phi la utilizatori este utilizarea bănci de condensatoare și compensatoare sincrone.
