Ce este o sursă electrică?

Omul modern întâlnește constant electricitatea în viața de zi cu zi și la locul de muncă, folosește dispozitive care consumă curent electric și dispozitive care îl generează. Când lucrați cu ei, ar trebui să țineți întotdeauna cont de capacitățile lor inerente caracteristicilor tehnice.

Unul dintre principalii indicatori ai oricărui dispozitiv electric este o astfel de mărime fizică precum energia electrică... Se obișnuiește să se numească intensitatea sau viteza de generare, transmitere sau conversie a energiei electrice în alte tipuri de energie, de exemplu, căldură, lumină, mecanic.

Transportul sau transferul energiei electrice mari în scopuri industriale se realizează conform linii electrice de înaltă tensiune.

Transformare energie electrica se realizează la posturile de transformare.

Consumul de energie electrică are loc în aparatele de uz casnic și industriale în diverse scopuri. Unul dintre tipurile lor comune sunt lămpi cu incandescență de diferite evaluări.

Puterea electrică a generatoarelor, liniilor electrice și consumatorilor din circuitele DC și AC are aceeași semnificație fizică, care este exprimată simultan în rapoarte diferite în funcție de forma semnalelor compozite. Pentru a defini modelele generale, noțiunile de valori instantanee... Ele subliniază din nou dependența ratei de transformare a energiei electrice în timp.

Determinarea puterii electrice instantanee

În electrotehnica teoretică, pentru a deriva relațiile de bază dintre curent, tensiune și putere, se folosesc imaginile acestora sub formă de valori instantanee, care sunt fixate la un anumit moment în timp.

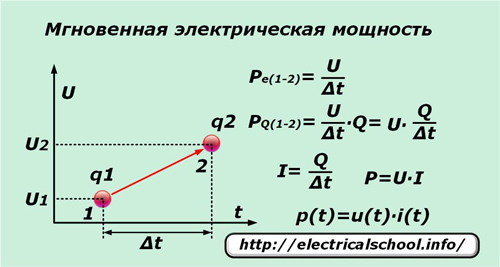
Dacă într-o perioadă foarte scurtă de timp ∆t o singură sarcină elementară q sub influența tensiunii U se deplasează din punctul «1» în punctul «2», atunci efectuează un lucru egal cu diferența de potențial dintre aceste puncte. Împărțind-o la intervalul de timp ∆t, obținem expresia pentru puterea instantanee pe unitatea de sarcină Pe (1-2).

Deoarece nu numai sarcina unică se mișcă sub acțiunea tensiunii aplicate, ci și toate cele adiacente care sunt sub influența acestei forțe, al cărei număr este reprezentat în mod convenabil de numărul Q, apoi valoarea instantanee a puterii PQ (1-2) pot fi scrise pentru ei.

După efectuarea unor transformări simple, obținem expresia puterii P și dependența valorii sale instantanee p (t) de componentele produsului dintre curentul instantaneu i (t) și tensiunea u (t).

Determinarea puterii electrice constante

V circuite DC magnitudinea căderii de tensiune în secțiunea circuitului și curentul care circulă prin aceasta nu se modifică și rămâne stabilă, egală cu valorile instantanee.Prin urmare, puterea din acest circuit poate fi determinată prin înmulțirea acestor valori sau împărțirea lucrării perfecte A la perioada de execuție a acesteia, așa cum se arată în imaginea explicativă.

Determinarea puterii electrice de curent alternativ

Legile variației sinusoidale a curenților și tensiunilor transmise prin rețelele electrice își impun influența asupra exprimării puterii în astfel de circuite. Aici intră în joc puterea aparentă, care este descrisă de triunghiul puterii și constă din componente active și reactive.

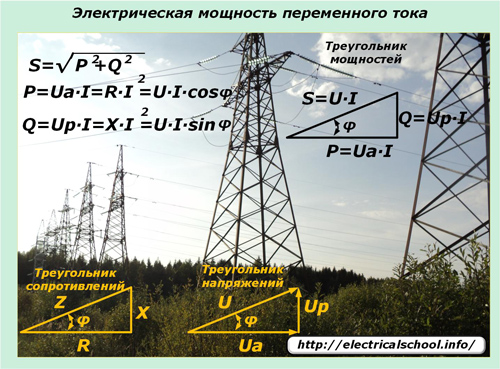
Un curent electric sinusoidal la trecerea prin liniile electrice cu tipuri mixte de sarcini în toate secțiunile nu schimbă forma armonicii sale.Și căderea de tensiune la sarcini reactive se schimbă în fază într-o anumită direcție. Expresiile valorii momentului ajută la înțelegerea efectului sarcinilor aplicate asupra schimbării puterii în circuit și a direcției acestuia.

În același timp, acordați imediat atenție faptului că direcția fluxului de curent de la generator la consumator și puterea transmisă prin circuitul creat sunt lucruri complet diferite, care în unele cazuri pot nu numai să nu coincida, ci și să fie îndreptate în direcții opuse.

Luați în considerare aceste relații în manifestarea lor ideală, pură pentru diferite tipuri de sarcini:

• activ;

• capacitiv;

• inductiv.

Disiparea puterii de sarcină activă

Vom presupune că generatorul produce o tensiune sinusoidală ideală u care se aplică rezistenței pur active a circuitului. Ampermetrul A și voltmetrul V măsoară curentul I și tensiunea U de fiecare dată când t.

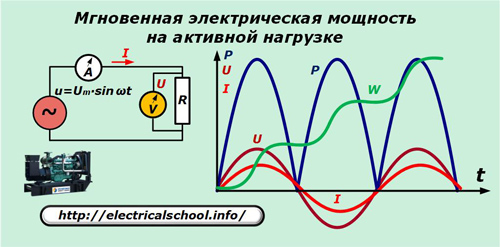
Graficul arată că sinusoidele curentului și căderea de tensiune pe rezistența activă se potrivesc în frecvență și fază, făcând aceleași oscilații. Forța exprimată de produsul lor oscilează la o frecvență dublă și rămâne întotdeauna pozitivă.

p = u ∙ i = Um ∙ sinωt ∙ Um / R ∙ sinωt = Um2/ R ∙ sin2ωt = Um2/ 2R ∙ (1-cos2ωt).

Dacă trecem la expresie tensiune de operare, atunci obținem: p = P ∙ (1-cos2ωt).

Vom integra apoi puterea pe perioada unei oscilații T și vom putea observa că câștigul de energie ∆W în acest interval crește. În timp, rezistența continuă să consume noi porțiuni de electricitate, așa cum se arată în grafic.

Cu sarcini reactive, caracteristicile consumului de energie sunt diferite, au o formă diferită.

Disiparea puterii capacitive

În circuitul electric al generatorului, înlocuiți elementul rezistiv cu un condensator de capacitate C.

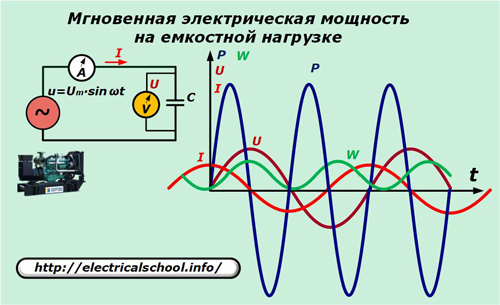
Relația dintre curent și scăderea de tensiune a capacității se exprimă prin raportul: I = C ∙ dU / dt = ω ∙ C ∙ Um ∙ cosωt.

Înmulțim valorile expresiilor instantanee ale curentului cu tensiunea și obținem valoarea puterii care este consumată de sarcina capacitivă.

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ Um ∙ cosωt = ω ∙ C ∙ Um2∙ sinωt ∙ cosωt = Um2/ (2X° C) ∙ sin2ωt = U2/ (2X° sin2) ωt

Aici puteți vedea că puterea fluctuează în jurul zero la frecvența de două ori mai mare decât tensiunea aplicată. Valoarea sa totală pentru perioada armonică, precum și câștigul de energie, este zero.

Aceasta înseamnă că energia se mișcă de-a lungul circuitului închis al circuitului în ambele direcții, dar nu funcționează.Un astfel de fapt se explică prin faptul că atunci când tensiunea sursei crește în valoare absolută, puterea este pozitivă, iar fluxul de energie prin circuit este direcționat către container, unde se acumulează energie.

După ce tensiunea trece la secțiunea armonică care scade, energia este returnată de la condensator la circuit la sursă. Nu se efectuează nicio lucrare utilă în niciunul dintre procese.

Disiparea puterii într-o sarcină inductivă

Acum, în circuitul de alimentare, înlocuiți condensatorul cu inductanța L.

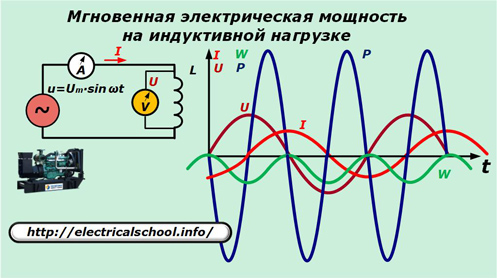
Aici curentul prin inductanță este exprimat prin raportul:

I = 1 / L∫udt = -Um / ωL ∙ cos ωt.

Apoi primim

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ (-Um / ωL ∙ cosωt) = — Um2/ ωL ∙ sinωt ∙ cosωt = -Um2/ (2ХL) ∙ sin2ωt = -U2ω)t (2.ХL2)t (2.ХL2)t

Expresiile rezultate ne permit să vedem natura schimbării direcției puterii și creșterea energiei pe inductanță, care efectuează aceleași oscilații care sunt inutile pentru a face lucru, ca și asupra capacității.

Puterea eliberată în sarcini reactive se numește componentă reactivă. În condiții ideale, atunci când firele de conectare nu au rezistență activă, acesta pare inofensiv și nu provoacă niciun rău. Dar în condiții reale de putere, tranzitorii periodici și fluctuațiile puterii reactive determină încălzirea tuturor elementelor active, inclusiv a firelor de conectare, pentru care se consumă o parte de energie și scade valoarea puterii complete aplicate a sursei.

Principala diferență între componenta reactivă a puterii este că nu efectuează deloc o muncă utilă, dar duce la pierderi de energie electrică și la sarcini în exces asupra echipamentelor, care sunt deosebit de periculoase în situații critice.

Din aceste motive, pentru a elimina influența puterii reactive, în special sisteme tehnice de compensare a acestuia.

Distribuția puterii la sarcină mixtă

Ca exemplu, folosim sarcina unui generator cu o caracteristică capacitivă activă.

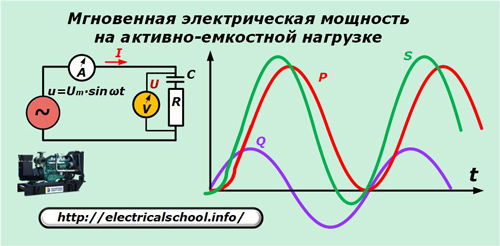
Pentru a simplifica imaginea, sinusoidele curenților și tensiunilor nu sunt afișate în graficul dat, dar trebuie avut în vedere că, având o natură activ-capacitivă a sarcinii, vectorul curent conduce tensiunea.

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ Im ∙ sin (ωt + φ).

După transformări obținem: p = P ∙ (1- cos 2ωt) + Q ∙ sin2ωt.

Acești doi termeni din ultima expresie sunt componentele active și reactive ale puterii aparente instantanee. Doar primul dintre acestea face o activitate utilă.

Instrumente de măsurare a puterii

Pentru a analiza consumul de energie electrică și a calcula pentru acesta, se folosesc dispozitive de măsurare, care au fost numite mult timp „Contoare”… Munca lor se bazează pe măsurarea valorilor efective ale curentului și tensiunii și înmulțirea automată a acestora cu o ieșire de informații.

Contoarele afișează consumul de energie prin numărarea timpului de funcționare al aparatelor electrice în mod incremental din momentul în care contorul este pornit sub sarcină.

Pentru a măsura componenta activă a puterii în circuitele de curent alternativ, wattmetre, și reactiv - varmetre. Au diferite denumiri de unitate:

• wați (W, W);

• var (var, var, var).

Pentru a determina consumul total de energie, este necesar să se calculeze valoarea acestuia folosind formula triunghiului de putere bazată pe citirile wattmetrului și varmetrului. Este exprimat în propriile sale unități - volți-amperi.

Denumirile acceptate ale unităților fiecăruia îi ajută pe electricieni să judece nu numai valoarea acesteia, ci și natura componentei de putere.