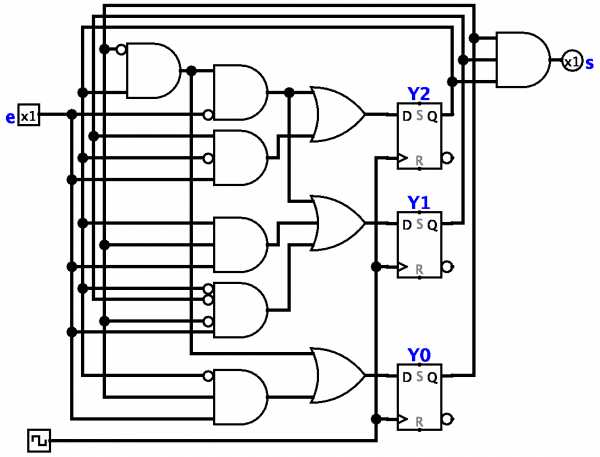
Teoria automatelor, automate finite
Structura, designul, principiul de funcționare a diferitelor mașini sunt în mare măsură determinate de scopul său funcțional. Distingeți între mașini tehnologice, de transport, de calcul, militare și alte mașini. Complexele automate întregi concepute pentru a efectua procese tehnologice complexe sunt introduse pe scară largă în diverse industrii. Sunt proiectate și construite automate care îndeplinesc diverse funcții logice (mașini logice).
Teoria automatelor — sectia de cibernetica, care a apărut sub influența cerințelor tehnologiei calculatoarelor digitale și a mașinilor de control. Automatele discrete studiate în teoria automatelor sunt modele abstracte ale sistemelor reale (atât tehnice, cât și biologice) care procesează informații discrete (digitale) în pași de timp discreti.
Teoria automatelor se bazează pe concepte matematice precise care formalizează idei intuitive despre funcționarea (comportamentul) automatului și despre structura acestuia (structura internă).
În acest caz, transformarea informațiilor este întotdeauna înțeleasă ca o operație care transformă secvențe de intrare compuse din litere din alfabetul de intrare în secvențe de ieșire compuse din litere din alfabetul de ieșire.
Aparatul de logică matematică, algebră, teoria probabilității, combinatorică și teoria grafurilor este utilizat pe scară largă.
Problema cu teoria automatelor în unele dintre părțile sale (teoria structurală a automatelor) a crescut din teoria circuitelor releu-contact, care a început să prindă contur la sfârșitul anilor 1930. inclusiv metode ale algebrei logice.

În teoria structurală a automatelor sunt studiate diferite tipuri de scheme, concepute pentru a descrie modul în care un automat complex este creat din componente (elemente) mai simple conectate corespunzător într-un sistem.
O altă direcție, numită teoria abstractă a automatelor, studiază comportamentul automatelor (adică natura transformării informațiilor efectuate de aceștia), făcând abstracție de specificul structurii lor interne și a apărut în anii 1950.
În cadrul teoriei abstracte a automatelor, conținutul conceptelor „automat” și „mașină” este epuizat în esență de descrierea standard a transformării informațiilor care este efectuată de un automat. O astfel de transformare poate fi deterministă, dar poate fi și probabilistică în natură.
Cele mai studiate sunt mașinile deterministe (automate), care includ automate finite — principalul obiect de studiu în teoria automatelor.
O mașină cu stări finite este caracterizată de o cantitate limitată de memorie (numărul de stări interne) și este definită folosind o funcție de tranziție.Cu o oarecare idealizare rezonabilă, toate mașinile matematice moderne și chiar creierul, din punctul de vedere al funcționării lor, pot fi considerate automate finite.
Termenii „mașină secvențială”, „automat Milly”, „automat Moore” sunt folosiți în literatură (și nu în mod uniform de către toți autorii) ca sinonime ale termenului „automat finit” sau pentru a sublinia anumite trăsături în funcțiile de tranziție ale unui finit. automat.
Automatele cu memorie nelimitată este o mașină Turing capabilă să realizeze (potențial) orice transformare eficientă a informațiilor. Conceptul de „mașină Turing” a apărut mai devreme decât conceptul de „mașină cu stări finite” și este studiat în principal în teoria algoritmilor.
Teoria abstractă a automatelor este strâns legată de teoriile algebrice binecunoscute, de exemplu teoria semigrupurilor. Din punct de vedere aplicativ, sunt de interes rezultatele care caracterizează transformarea informaţiei într-un automat în ceea ce priveşte dimensiunea memoriei.
Este cazul, de exemplu, în problemele cu experimente pe automate (lucrări ale lui E.F. Moore etc.), unde una sau alta informație despre funcțiile de tranziție ale automatului sau despre capacitatea memoriei acestuia se obține din rezultatele experimente.
O altă sarcină este de a calcula perioadele secvențelor de ieșire, pe baza informațiilor disponibile despre dimensiunea memoriei automatului și perioadele secvențelor de intrare.
De mare importanță este dezvoltarea unor metode de minimizare a memoriei mașinilor cu stări finite și studierea comportamentului acestora în medii aleatorii.
În teoria automatelor abstracte, problema de sinteză este următoarea.În ceea ce privește un limbaj clar formalizat, condițiile sunt scrise pentru comportamentul automatului proiectat (pentru evenimentul reprezentat în automat). În acest caz, este necesar să se dezvolte metode care, în funcție de fiecare condiție scrisă:
1) aflați dacă există o astfel de mașină de stări încât informația transformată de ea să îndeplinească această condiție;
2) dacă da, atunci se construiesc funcțiile de tranziție ale unei astfel de mașini cu stări finite sau se estimează dimensiunea memoriei acesteia.
Rezolvarea sarcinii de sinteză într-o astfel de formulare presupune crearea preliminară a unui limbaj convenabil pentru înregistrarea condițiilor de funcționare a unui automat cu algoritmi convenabil pentru trecerea de la funcții de înregistrare la funcții tranzitive.
În teoria structurală a automatelor, problema de sinteză constă în construirea unui lanț de elemente de un tip dat care realizează un automat finit dat de funcțiile sale de tranziție. În acest caz, de obicei ei stabilesc un anumit criteriu de optimitate (de exemplu, numărul minim de elemente) și caută să obțină o schemă optimă.
După cum s-a dovedit mai târziu, aceasta înseamnă că unele dintre metodele și conceptele dezvoltate mai devreme în legătură cu circuitele releu-contact sunt aplicabile circuitelor de alt tip.
În legătură cu dezvoltarea tehnologiilor electronice, cele mai răspândite sunt schemele a elementelor functionale (rețele logice). Un caz special de rețele logice sunt rețelele neuronale abstracte, ale căror elemente se numesc neuroni.
Au fost dezvoltate multe metode de sinteză, în funcție de tipul de circuite și de transformarea informațiilor pentru care sunt destinate (Sinteza dispozitivelor relee).
Uite -Minimizarea circuitelor combinaționale, hărți Carnot, sinteza circuitelor
Mașină cu stări finite — un model matematic al unui sistem de control cu o dimensiune de memorie fixă (incapabilă de a crește în timpul funcționării).
Conceptul de mașină cu stări finite este o abstractizare matematică care caracterizează caracteristicile generale ale unui set de sisteme de control (de exemplu, un dispozitiv de releu cu mai multe bucle). Toate astfel de sisteme au caracteristici comune care este firesc să fie acceptate ca definiție a unui automat finit.
Fiecare automat finalizat are o intrare expusă influențelor externe și elementelor interne. Atât pentru elementele de intrare, cât și pentru elementele interne, există un număr fix de stări discrete pe care le pot lua.
Schimbarea stărilor elementelor de intrare și interne are loc în momente discrete de timp, intervalele dintre care se numesc căpușe. Starea internă (starea elementelor interne) la sfârșitul benzii este determinată în întregime de starea internă și de starea intrării la începutul benzii.
Toate celelalte definiții ale unui automat finit pot fi reduse la această caracteristică, în special definiții care presupun că un automat finit are o ieșire care depinde de starea internă a automatului la un moment dat.
În ceea ce privește o astfel de caracteristică, natura intrărilor și stărilor sale interne este irelevantă pentru descrierea unui automat complet. În loc de intrări și stări, puteți doar să vă uitați la numerele lor într-o numerotare aleatorie.
Mașina de stări va fi setată dacă este specificată dependența numărului său intern de stare de numărul de stare intern anterior și de numărul de stare de intrare anterior. O astfel de sarcină poate fi sub forma unui tabel final.
Un alt mod comun de a defini un automat complet este construcția așa-numitului diagrame de tranziție. Stările de intrare sunt adesea numite pur și simplu intrări, iar stările interne sunt pur și simplu stări.
O mașină cu stări finite poate fi un model atât al dispozitivelor tehnice, cât și al unor sisteme biologice. Automatele de primul tip sunt, de exemplu, dispozitivele releu și diverse calculatoare electronice, incl. controlere logice programabile.
În cazul unui dispozitiv releu, rolul stărilor de intrare este jucat de combinații de stări ale elementelor sensibile ale dispozitivului releu (fiecare combinație de astfel de stări este o „stare complexă”, caracterizată prin indicarea tuturor elementelor sensibile ale aceste stări discrete pe care le au într-un moment dat). În mod similar, combinațiile de stări ale elementelor intermediare ale unui dispozitiv releu acționează ca stări interne.
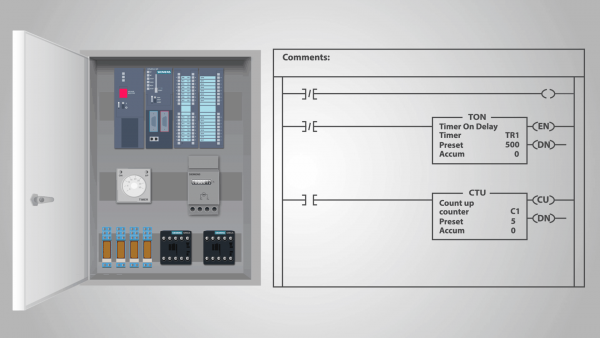
Un controler logic programabil (PLC) este un exemplu de dispozitiv de acțiune releu care poate fi numit o mașină de stare autonomă.
De fapt, odată ce programul a fost introdus în PLC și controlerul a început să calculeze, acesta nu este expus influențelor externe și fiecare stare ulterioară este complet determinată de starea anterioară. Putem presupune că intrarea are aceeași stare în fiecare ciclu de ceas.
Dimpotrivă, orice mașină cu stări finite care are singura stare posibilă de intrare este în mod natural numită autonomă, deoarece în acest caz mediul extern nu poartă nicio informație care să-și controleze comportamentul.
Vezi si:
Utilizarea sistemelor cu microprocesoare în inginerie electrică pe exemplul utilizării PLC