Determinarea puterii motorului în timpul funcționării tranzitorii repetitive

Modul de funcționare a acționării electrice, în care perioadele de funcționare sunt de o asemenea durată și alternează astfel cu pauze de o anumită durată, încât temperatura tuturor dispozitivelor care compun acționarea electrică nu atinge o valoare stabilă, nici în timpul fiecărei perioade de muncă, nici în fiecare pauză nu se apelează la întrerupere.

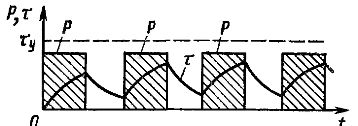
Regimul de încărcare periodică corespunde graficelor similare cu cele prezentate în Fig. 1. Supraîncălzirea motorului electric variază de-a lungul liniei întrerupte a unui ferăstrău format din segmente alternative de curbe de încălzire și răcire. Modul de încărcare intermitentă este tipic pentru majoritatea acționărilor mașinilor-unelte.

Orez. 1. Program de încărcare intermitentă

Puterea unui motor electric care funcționează în modul periodic este cel mai convenabil determinată de formula pentru pierderile medii, care poate fi scrisă ca

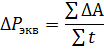
unde ΔA este pierderea de energie la fiecare valoare de sarcină, inclusiv procesele de pornire și oprire.

Când motorul electric nu funcționează, condițiile de răcire se deteriorează semnificativ. Acest lucru este luat în considerare prin introducerea coeficienților experimentali β0 <1. Timpul de pauză t0 se înmulțește cu coeficientul β0, în urma căruia numitorul formulei scade, iar pierderile echivalente ΔREKV cresc și, în consecință, puterea nominală a motorului electric crește.

Pentru motoarele asincrone protejate din seria A cu o turație sincronă de 1500 rpm și o putere de 1-100 kW, coeficientul β0 este de 0,50-0,17, iar pentru motoarele de purjare β0 = 0,45-0,3 (cu o creștere a Пн , coeficientul β0 scade). Pentru motoarele închise, β0 este aproape de unitate (0,93-0,98). Acest lucru se datorează faptului că eficiența ventilației motoarelor închise este scăzută.

La pornire și oprire, viteza medie a motorului electric este mai mică decât cea nominală, drept urmare și răcirea motorului electric se deteriorează, care se caracterizează prin coeficient

La determinarea coeficientului β1, se presupune condiționat că modificarea frecvenței de rotație are loc conform unei legi liniare și că coeficientul β1 depinde liniar de aceasta.

Cunoscând coeficienții β0 și β1, obținem

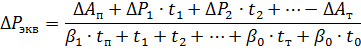
unde ΔР1, ΔР2, — pierderi de putere la diferite sarcini, kW; t1 t2 — timpul de acțiune al acestor sarcini, s; tn, tT, t0 — timpul de pornire, întârziere și pauză, s; ΔАп ΔАТ — pierderi de energie în motor în timpul pornirii și opririi, kJ.

După cum sa menționat mai sus, fiecare motor trebuie selectat pentru condiții de încălzire și suprasarcină. Pentru a aplica metoda pierderilor medii, este necesar să se monteze în prealabil un anumit motor electric, care în acest caz se recomandă și să fie selectat în funcție de condițiile de suprasarcină.Formula de putere echivalentă poate fi utilizată pentru un calcul grosier în cazurile în care pornirea și oprirea sunt rare și nu afectează semnificativ încălzirea motorului electric.

În inginerie mecanică, pentru funcționarea în regim de sarcină intermitentă, se folosesc motoare electrice proiectate să funcționeze cu o sarcină continuă. Industria electrică produce și motoare special concepute pentru a face față sarcinilor intermitente, care sunt utilizate pe scară largă în structurile de ridicare și transport. Astfel de motoare electrice sunt selectate ținând cont de durata relativă de includere:

unde tp este timpul de funcționare a motorului; t0 — durata pauzei.

Un exemplu de alegere a unui motor în funcție de putere în modul de funcționare multiplu pe termen scurt.

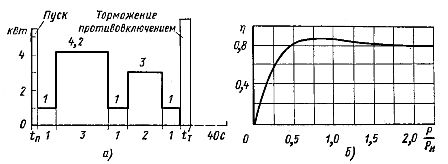
Determinați puterea motorului electric la n0 — 1500 rpm; motorul funcționează conform programului de sarcină prezentat în fig. 2, a. Puterea arborelui motorului electric la mașina în gol Pxx = 1 kW. Momentul de inerție redus al mașinii Jc = 0,045 kg-m2.

Răspuns:

1. Preselectați motorul electric în funcție de condițiile de suprasarcină, cum ar fi λ = 1,6:

Conform catalogului, alegem un motor electric cu varianta protejată de cea mai apropiată putere mare (2,8 kW), în care mon = 1420 rpm;

Pentru acest motor λ = 0,85 • 2 = 1,7. În acest fel, motorul este selectat cu o anumită limită de suprasarcină.

Dependența η = f (P / Pн) a acestui motor este prezentată în fig. 2, b.

Orez. 2. Dependențe N = f (t) și η = f (P / Pн)

2. Conform formulei

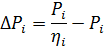
detectăm pierderi la puterile 1; 3; 4,2 kW (la program). Pierderile sunt respectiv 0,35; 0,65 și 1 kW. Găsim pierderi la Pn = 2,8 kW, care sunt ΔPn = 0,57 kW.

3. Determinați ora de începere și ora de oprire prin opoziție:

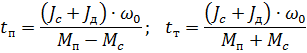
Unde:

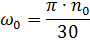
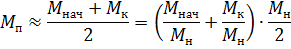
Se obține tn = 0,30 s; tt = 0,21 s.

4. Determinați pierderile de pornire și de oprire:

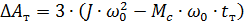
Se obține ΔAp = 1,8 kJ și ΔAt = 3,8 kJ.

5. Găsiți pierderile echivalente în buclă:

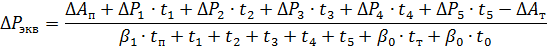
Unde

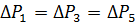
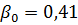
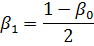
Se obține ΔREKV = 0,44 kW. Deoarece ΔPn = 0,57, atunci ΔREKV <ΔPn și, prin urmare, motorul este selectat corect.