Calculul capacității condensatorului

Capacitatea C este capacitatea condensatorului de a accepta (stocare și reține) cantitatea de electricitate Q în amperi-secunde sau sarcina Q în pandantive. Dacă îi spuneți unui corp, de exemplu o minge, o sarcină electrică (cantitate de electricitate) Q, atunci un electroscop conectat între acest corp și pământ va afișa o tensiune U (Fig. 1). Această tensiune este proporțională cu sarcina și depinde, de asemenea, de forma și dimensiunea corpului.

Relația dintre sarcina Q și tensiunea U este exprimată prin formula Q = C ∙ U.

Constanta de proporționalitate C se numește capacitatea corpului. Dacă corpul are forma unei bile, capacitatea corpului este proporțională cu raza bilei r.

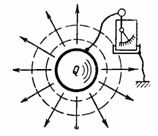
Orez. 1.

Unitatea de măsură a capacității este faradul (F).

Corpul are o capacitate de 1 F când o sarcină de 1 k produce o tensiune de 1 V. între el și pământ. Farazii sunt o unitate de măsură foarte mare, așa că în practică se folosesc unități mai mici: microfarad (μF), nanofarad (nF) și picofarad (pF)...

Aceste unități sunt legate prin următoarele rapoarte: 1 Ф = 10 ^ 6 μF; 1 μF = 10 ^ 6 pF; 1 nF = 10 ^ 3 pF.

Capacitatea unei bile cu raza de 1 cm este de 1,1 pF.

Nu numai un corp izolat poate acumula încărcare, ci și un dispozitiv special numit condensator. Un condensator este format din două sau mai multe plăci (plăci) care sunt separate printr-un dielectric (izolație).

În fig. 2 prezintă un circuit cu o sursă de curent continuu conectată la un condensator. Când este pornit, se formează o sarcină pozitivă +Q în placa din dreapta a condensatorului și o sarcină negativă -Q în placa din stânga. Pe parcursul încărcarea condensatorului un curent trece prin circuit, care se oprește după terminarea încărcării; atunci tensiunea pe condensator va fi egală cu e. etc. c. sursa U. Sarcina de pe placa condensatorului, tensiunea si capacitatea sunt legate de raportul Q = C ∙ U. In acest caz se formeaza un camp electrostatic in dielectricul condensatorului.

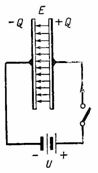
Orez. 2.

Capacitatea unui condensator cu un dielectric de aer poate fi calculată prin formula C = S / (4 ∙ π ∙ d) ∙ 1,11, pF, unde S este aria unei plăci, cm2; d este distanța dintre plăci, cm; C este capacitatea condensatorului, pF.

Capacitatea unui condensator format din n plăci (Fig. 3) este egală cu: C = (n-1) ∙ S / (4 ∙ π ∙ d) ∙ 1,11, pF.

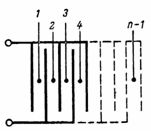
Orez. 3.

Dacă spațiul dintre plăci este umplut cu un alt dielectric, de exemplu hârtie, capacitatea condensatorului va crește cu un factor de ε. Când se folosește izolație din hârtie, capacitatea va crește de 3 ori, cu izolație de mică - de 5-8 ori, cu sticlă - de 7 ori etc. Valoarea lui ε se numește constanta dielectrică a dielectricului.

Formula generală de determinare a capacității unui condensator cu constantă dielectrică ε (epsilon) este: C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1,11, pF.

Această formulă este utilă pentru calcularea condensatoarelor variabile mici pentru radiouri.Aceeași formulă poate fi reprezentată ca: C = (ε_0 ∙ ε ∙ S) / d, unde ε_0 este constanta dielectrică sau constanta dielectrică a vidului (ε_0 = 8.859 ∙ 10 ^ (- 12) F / m); ε este constanta dielectrică a dielectricului.

În această formulă, dimensiunile sunt înlocuite în metri, iar capacitatea se obține în faradi.

Exemple de

1. Care este capacitatea planetei Pământ, a cărei rază este r = 6378 km?

Deoarece capacitatea unei sfere cu raza de 1 cm este egală cu 1,11 pF, capacitatea Pământului este: C = 637,8 ∙ 10 ^ 6 ∙ 1,11 = 707,95 ∙ 10 ^ 6 pF = 708 μF. (Capacitatea unei mingi de dimensiunea planetei noastre este relativ mică. Condensatoarele electrolitice de dimensiuni mici au această capacitate).

2. Determinați capacitatea unui condensator format din două plăci, fiecare având o suprafață S = 120 cm2.

Plăcile sunt separate de un strat de aer cu grosimea d = 0,5 cm, C = S / (4 ∙ π ∙ d) ∙ 1,11 = (120 ∙ 1,11) / (4 ∙ π ∙ 0,5) = 21 ,20 pF .. .

3. Determinați capacitatea condensatorului cu datele date în exemplul anterior, dacă spațiul dintre plăci este umplut cu hârtie ceară cu constantă dielectrică ε = 4, sticlă (ε = 7), carton electric (ε = 2) , mica (ε = 8).

Un condensator de hârtie ceară are o capacitate C = ε ∙ (S ∙ 1,11) / (4 ∙ π ∙ d) = 4 ∙ 21,2 = 84,8 pF.

Capacitatea unui condensator de sticlă este C = 7 ∙ 21,2 = 148,4 pF.

Capacitatea condensatorului din carton este C = 2 ∙ 21,2 = 42,3 pF.

Capacitatea condensatorului de mica este C = 8 ∙ 21,2 = 169,6 pF.

4. Care este capacitatea unui condensator rotativ de aer pentru un receptor radio format din 20 de plăci cu o suprafață de 20 cm2 dacă distanța dintre plăci este de 0,06 cm (Fig. 149)?

C = (n-1) ∙ (S ∙ 1,11) / (4 ∙ π ∙ d) = (20-1) ∙ (20 ∙ 1,11) / (4 ∙ π ∙ 0,06) = 559, 44 pF.

Condensatorul prezentat în fig.3, constă din cele mai simple condensatoare separate cu două plăci, al căror număr este egal cu n-1.

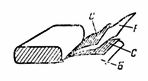
5. Un condensator de hârtie de capacitate C = 2 μF este format din două benzi de folie de cositor C și două benzi dintr-un dielectric din hârtie ceară B cu o constantă dielectrică ε = 6. Grosimea hârtiei cerate este d = 0,1 mm. Benzile pliate sunt rulate, cablurile sunt realizate din plăci de oțel. Determinați lungimea benzii de oțel a condensatorului dacă lățimea acesteia este de 4 cm (Fig. 4).

Orez. 4.

Mai întâi, determinăm aria unei benzi cu formula C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1.11, de unde S = (C ∙ 4 ∙ π ∙ d) / (ε ∙ 1.11) = ( 2 ∙ 4 ∙ π ∙ 0,01 ∙ 10 ^ 6) / (6 ∙ 1,11); S = 2.000.000 / (6 ∙ 1,11) ∙ 4 ∙ π ∙ 0,01 = 37680 cm2.

Lungimea fiecărei benzi este l = 37680/4 = 9420 cm = 94,2 m.